Tutorial 1.1: Pattern search-based two level optimization
Contents
Tutorial 1.1: Pattern search-based two level optimization#
Authors: Xiaoyu Xie
Contact: xiaoyuxie2020@u.northwestern.edu
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import ParameterGrid
from sklearn.model_selection import train_test_split
from scipy.optimize import minimize
from sklearn.preprocessing import PolynomialFeatures
from sklearn.utils import shuffle
%matplotlib inline
# plt.rcParams["font.family"] = 'Arial'
np.set_printoptions(suppress=True)
# # please uncomment these two lines, if you run this code in Colab
# !git clone https://github.com/xiaoyuxie-vico/PyDimension-Book
# %cd PyDimension-Book/examples
Helper functions#
class Dataset(object):
'''
Load and parse dataset
'''
def __init__(self, dataset_path, input_list, output_list):
self.dataset_path = dataset_path
self.input_list, self.output_list = input_list, output_list
self.df = self._load_dataset()
self.df_train, self.df_test = self._split_dataset()
def _load_dataset(self):
'''load dataset'''
df = pd.read_csv(self.dataset_path)
return df
def _split_dataset(self, test_size=0.2, random_state=1):
'''randomly split dataset'''
df_train, df_test = train_test_split(self.df, test_size=test_size, random_state=random_state)
return df_train, df_test
def parser(self, is_shuffle=True, random_state=0):
'''load dataset using numpy'''
X_train = self.df_train[self.input_list].to_numpy()
y_train = self.df_train[self.output_list].to_numpy().reshape(-1,)
X_test = self.df_test[self.input_list].to_numpy()
y_test = self.df_test[self.output_list].to_numpy().reshape(-1,)
# shuffle
X_train, y_train = shuffle(X_train, y_train, random_state=random_state)
return X_train, y_train, X_test, y_test
dataset_path = '../dataset/dataset_keyhole.csv'
input_list = ['etaP', 'Vs', 'r0', 'alpha', 'rho', 'cp', 'Tl-T0']
output_list = ['e*']
data_loader = Dataset(dataset_path, input_list, output_list)
X_train, y_train, X_test, y_test = data_loader.parser()
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)
(72, 7) (72,) (18, 7) (18,)
class DimensionlessLearning(object):
'''
Indentify the explicit form one coefficient using dimensionless learning
'''
def __init__(self, X, y, scaling_mat):
super(DimensionlessLearning, self).__init__()
self.X, self.y = X, y
self.scaling_mat = scaling_mat
self.basis_num = scaling_mat.shape[1]
def parse_power_index(self, basis_coef):
'''
parse power index based on basis coefficients
'''
power_index = np.sum(np.multiply(self.scaling_mat, basis_coef), axis=1)
return power_index
def scale_input(self, X, basis_coef):
'''
scale the the input data into a few dimensionless numbers
'''
power_index = self.parse_power_index(basis_coef)
X_scaled = np.prod(np.power(X, power_index), axis=1)
return X_scaled, power_index
def parse_feats(self, X, deg=5):
'''
prepare different degrees' features
'''
poly = PolynomialFeatures(deg)
X_poly = poly.fit_transform(X.reshape(-1, 1))
return X_poly
def predict(self, X, power_index, scaling_coef, deg=5):
'''
based on learned basis coefficients and scaling coefficients to predict
'''
X_scaled = np.prod(np.power(X, power_index), axis=1)
X_poly = self.parse_feats(X_scaled, deg)
pred = np.sum(np.multiply(X_poly, scaling_coef), axis=1)
return pred
def fit(self, method='pattern_search', init_point_num=20, seed=0):
'''
fit the data
'''
BASE = 2 ** 20
r2, basis_coef, scaling_coef = 0, None, None
for idx in range(init_point_num):
seed = (idx + seed * init_point_num) % BASE
if method == 'pattern_search':
r2_temp, basis_coef_temp, scaling_coef_temp = self.fit_pattern_search(seed=seed)
elif method == 'gradient_descent':
r2_temp, basis_coef_temp, scaling_coef_temp = self.fit_gradient_descent(seed=seed)
print('r2_temp, basis_coef_temp, scaling_coef_temp', r2_temp, basis_coef_temp, scaling_coef_temp)
else:
raise Exception('Error in the optimizaiton method')
if r2_temp < r2:
continue
r2, basis_coef, scaling_coef = r2_temp, basis_coef_temp, scaling_coef_temp
return r2, basis_coef, scaling_coef
def _opt(self, basis_coef):
'''
fit a linear regression
'''
# prepare polynomial features based on dimensionless numbers
X_scaled, power_index = self.scale_input(self.X, basis_coef)
X_poly = self.parse_feats(X_scaled)
# fit a polynomial
reg = LinearRegression(fit_intercept=False)
reg.fit(X_poly, self.y)
y_pred = reg.predict(X_poly)
r2 = r2_score(self.y, y_pred)
scaling_coef = reg.coef_
return r2, power_index, scaling_coef
def fit_pattern_search(self, gamma0=0.5, max_iter=10, grid_range=[-2, 2], grid_interval=0.5, clip_threshold=0.2, seed=0):
'''
pattern search-based optimization
Args:
gamma0 [float]: basis coefficient for the first basis vector;
max_iter [int]: the maximum iteration for pattern search;
grid_range [list of int]: the range for each basis coefficient;
grid_interval [float]: the grid interval for each basis coefficient;
clip_threshold [float]: if the R2 score for the initial point is lower than this threshold, break the loop;
Return:
r2 [float]: the final R2 score
power_index [array]: the power law index for one input dimensionless nunber
scaling_coef [array]: the scaling law coefficients
'''
def _get_coordinates(basis_num, basis_coef, grid_interval):
'''
build a list to store all possible coordiantes
'''
# prepare grid
param_grid = {}
center_coord = []
coord_all = []
for i in range(basis_num):
gamma_value = basis_coef[i]
param_grid[f'gamma{i}'] = [gamma_value-grid_interval, gamma_value, gamma_value+grid_interval]
center_coord.append(gamma_value)
# build grid
grid = ParameterGrid(param_grid)
for params in grid:
coord = []
for i in range(basis_num):
coord.append(params[f'gamma{i}'])
if coord != center_coord:
coord_all.append(coord)
return coord_all
def _init_basis_coef(basis_num, grid_range, grid_interval, gamma0):
'''
initialize basis coefficient
'''
grid_num = int((grid_range[1] - grid_range[0]) / grid_interval + 1)
basis_coef = np.zeros((basis_num))
for i in range(basis_num):
basis_coef[i] = np.random.choice(np.linspace(grid_range[0], grid_range[1], grid_num), 1)[0] # [-2, 2]
# basis_coef[i] = 1
basis_coef[0] = gamma0
return basis_coef
# initial basis coefficients
np.random.seed(seed)
basis_coef = _init_basis_coef(self.basis_num, grid_range, grid_interval, gamma0)
# randomly initialize different center points
iter_num = 0
while iter_num < max_iter:
candidate_coord = _get_coordinates(self.basis_num, basis_coef, grid_interval)
# calculate the center point
r2_center, power_index_center, scaling_coef_center = self._opt(basis_coef)
# print('r2_center', round(r2_center, 4), 'power_index_center', [round(each, 2) for each in list(power_index_center.reshape(-1,))])
# break if the initial point has a low R2 score
if r2_center < clip_threshold:
break
# calculate the neighboring points
r2_bounds_val = []
for gamma_list in candidate_coord:
basis_coef_temp = np.array(gamma_list)
r2_bound, power_index_bound, scaling_coef_bound = self._opt(basis_coef_temp)
r2_bounds_val.append(r2_bound)
# sort the R2 score for neighboring points from high to low
highest_index = np.argsort(r2_bounds_val)[::-1][0]
iter_num += 1
# udpate the center coordiantes if the neighboring point has a higher R2 score
if r2_center < r2_bounds_val[highest_index]:
basis_coef = np.array(candidate_coord[highest_index])
power_index = self.parse_power_index(basis_coef)
# res_info = {'gamma_list': gamma_list, 'r2_center': round(r2_bounds_val[highest_index], 4)}
else:
break
# calcualte the final R2 and coefficients
r2, power_index, scaling_coef = self._opt(basis_coef)
return r2, power_index, scaling_coef
def test_keyhole_example(method):
'''
keyhole problem
'''
################################### config ###################################
dataset_path = '../dataset/dataset_keyhole.csv'
input_list = ['etaP', 'Vs', 'r0', 'alpha', 'rho', 'cp', 'Tl-T0']
output_list = ['e*']
# dimension matrix
D_in = np.array(
[
[2., 1., 1., 2., -3., 2., 0.],
[-3., -1., 0., -1., 0., -2., 0.],
[1., 0., 0., 0., 1., 0., 0.],
[0., 0., 0., 0., 0., -1., 1.],
],
)
# best weights for Ke: 0.5, 1, 1
# basis vectors in columns
scaling_mat = np.array(
[
[0., 0., 1],
[1, 2., -3],
[1, 0., -2.],
[-1, 0., 0.],
[0., 0., -1],
[0., -1, 0.],
[0., -1, 0.]],
)
deg = 5
################################### dataset ########################################
# load, split, and shuffle the dataset
data_loader = Dataset(dataset_path, input_list, output_list)
X_train, y_train, X_test, y_test = data_loader.parser()
print(f'[Dataset] X_train: {X_train.shape}, y_train: {y_train.shape}')
print(f'[Dataset] X_test: {X_test.shape}, y_test: {y_test.shape}')
################################### training and testing ###########################
print('[Training]')
dimensionless_learning = DimensionlessLearning(X_train, y_train, scaling_mat)
r2, power_index, scaling_coef = dimensionless_learning.fit(method=method)
print(f'Final r2: {r2:.4f}, power_index: {power_index}, scaling_coef: {scaling_coef}')
pred_train = dimensionless_learning.predict(X_train, power_index, scaling_coef, deg)
pred_test = dimensionless_learning.predict(X_test, power_index, scaling_coef, deg)
################################### visualization ###################################
print('[Visualization]')
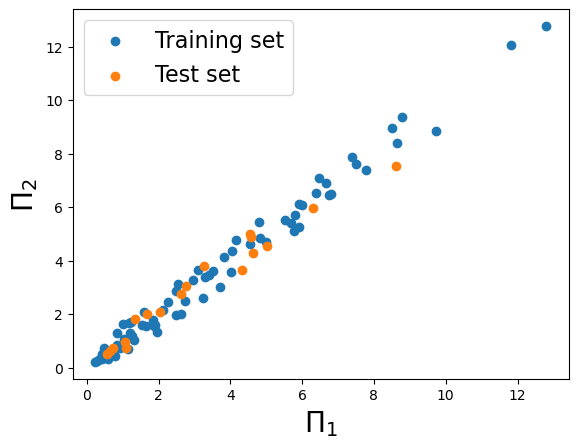
fig = plt.figure()
plt.scatter(pred_train, y_train, label='Training set')
plt.scatter(pred_test, y_test, label='Test set')
plt.legend(fontsize=16)
plt.xlabel(r'$\Pi_1$', fontsize=20)
plt.ylabel(r'$\Pi_2$', fontsize=20)
plt.show()
method = 'pattern_search'
test_keyhole_example(method)
[Dataset] X_train: (72, 7), y_train: (72,)
[Dataset] X_test: (18, 7), y_test: (18,)
[Training]
Final r2: 0.9841, power_index: [ 1. -0.5 -1.5 -0.5 -1. -1. -1. ], scaling_coef: [-0.14717067 0.06325514 0.0038886 -0.00009134 0.00000091 -0. ]
[Visualization]