1Data-Driven Discovery of Universal Laws

We develop data-driven frameworks that automatically discover fundamental physical laws, dimensionless numbers, and scaling relationships from experimental measurements. Our approach integrates classical dimensional analysis with modern machine learning to extract interpretable physical insights from high-dimensional, noisy experimental data. This research direction encompasses three key contributions: the foundational dimensionless learning framework, an enhanced tutorial with geometric interpretation, and a dimensionally invariant neural network architecture.

Dimensionless Learning: Dimensional Analysis + Machine Learning

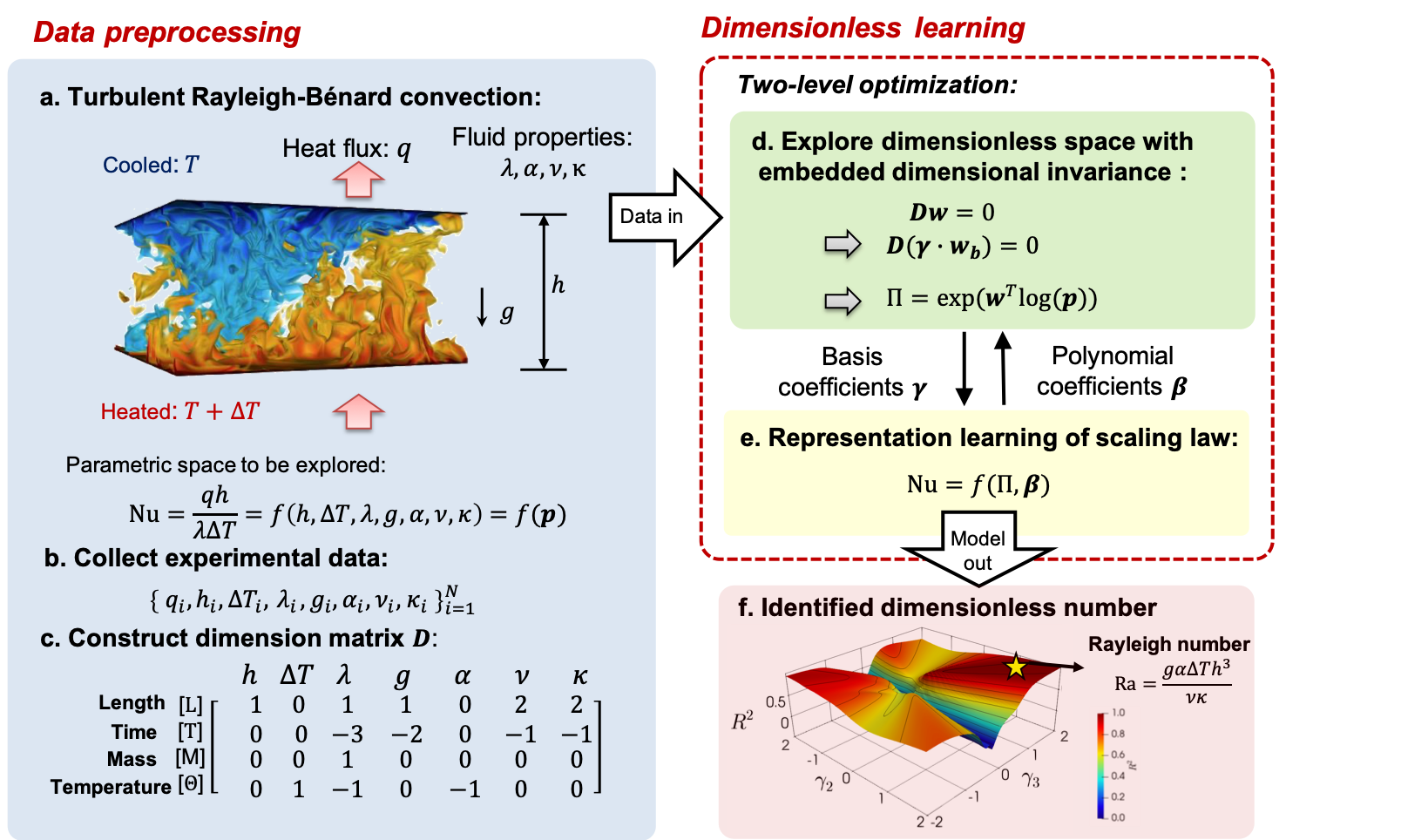
We introduce dimensionless learning, a mechanistic data-driven framework that embeds the principle of dimensional invariance into a two-level machine learning scheme. The method automatically discovers dominant dimensionless numbers and governing laws—including scaling laws and differential equations—directly from noisy and scarce experimental measurements. By enforcing dimensional consistency as a physical constraint, the framework achieves superior interpretability and generalizability compared to purely data-driven approaches.

Tutorial on Dimensionless Learning 2.0: Geometric Interpretation and the Effect of Noise

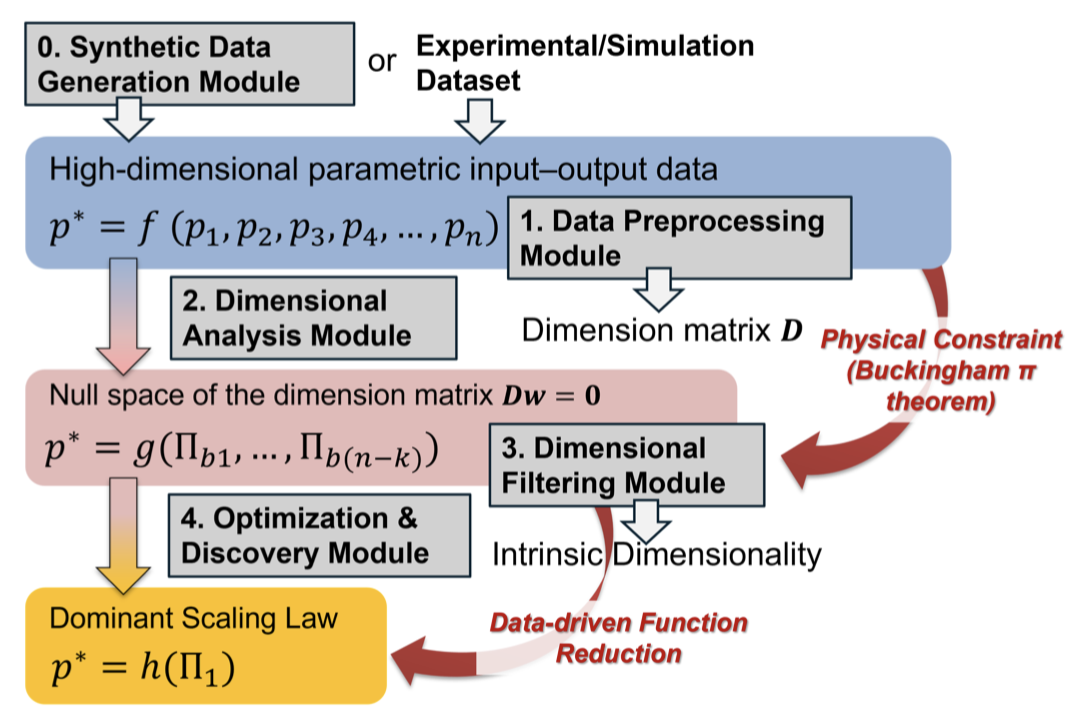
We present an enhanced tutorial that provides comprehensive geometric interpretation of dimensionless learning and systematic analysis of its robustness to measurement noise. This tutorial (PyDimension 2.0) offers deeper theoretical insights into how dimensionless numbers emerge from high-dimensional parameter spaces and demonstrates the method's effectiveness under various noise conditions and data sampling scenarios. It serves as both an educational resource and a practical guide for researchers applying dimensionless learning to experimental data.

Dimensionally Invariant Neural Network (DimensionNet)

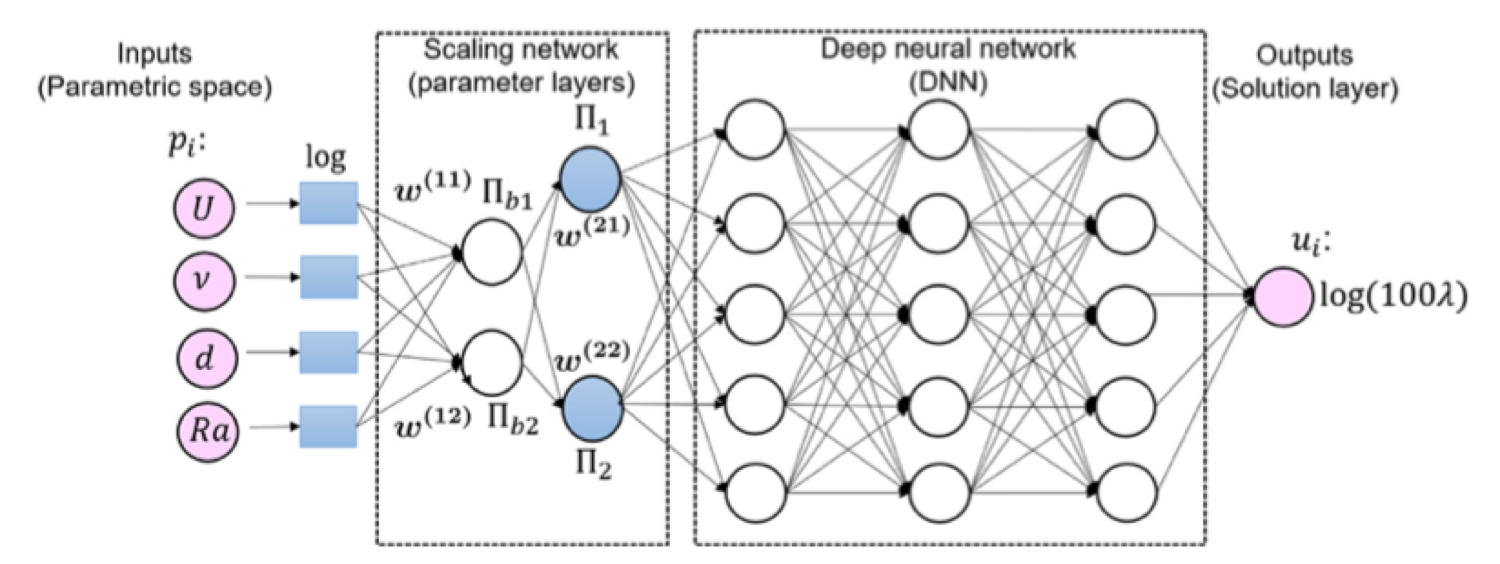
We develop the Dimensionally Invariant Neural Network (DimensionNet) as part of the Hierarchical Deep Learning Neural Network (HiDeNN) framework. DimensionNet automatically discovers a reduced set of governing dimensionless numbers from high-dimensional input parameters and performs learning in the dimensionless space. This architecture achieves significant dimensionality reduction while preserving physical interpretability, enabling efficient and accurate predictions for complex physical systems with many input variables.

2Data-Driven Reduced-Order Modeling

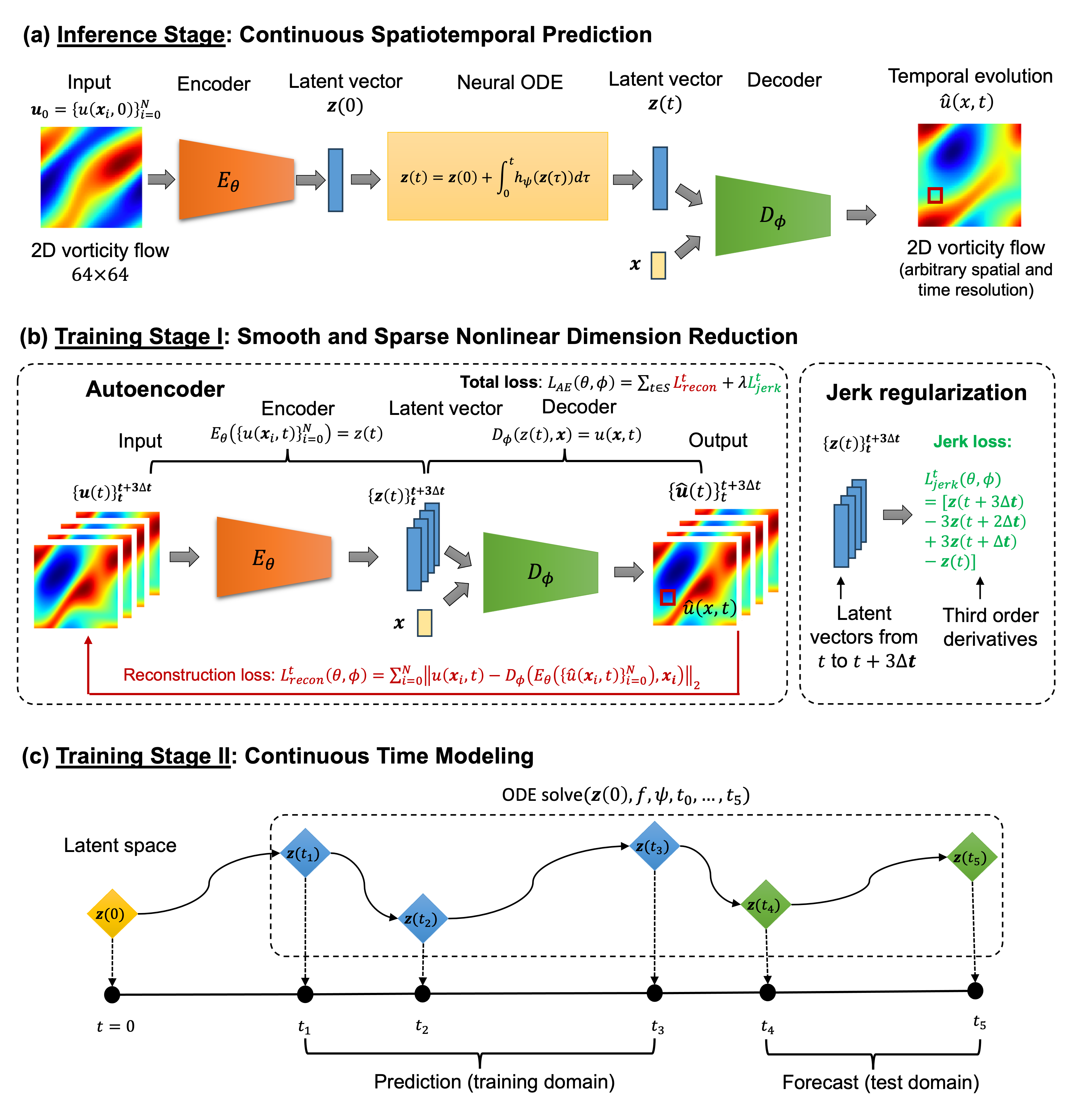
Smooth and Sparse Latent Dynamics in Operator Learning with Jerk Regularization

Spatiotemporal modeling is critical for understanding complex systems across various scientific and engineering disciplines, but governing equations are often not fully known or computationally intractable due to inherent system complexity. Data-driven reduced-order models (ROMs) offer a promising approach for fast and accurate spatiotemporal forecasting by computing solutions in a compressed latent space.

However, these models often neglect temporal correlations between consecutive snapshots when constructing the latent space, leading to suboptimal compression, jagged latent trajectories, and limited extrapolation ability over time. To address these issues, this paper introduces a continuous operator learning framework that incorporates jerk regularization into the learning of the compressed latent space. This jerk regularization promotes smoothness and sparsity of latent space dynamics, which not only yields enhanced accuracy and convergence speed but also helps identify intrinsic latent space coordinates.

The framework consists of an implicit neural representation (INR)-based autoencoder and a neural ODE latent dynamics model, allowing for inference at any desired spatial or temporal resolution. The effectiveness of this framework is demonstrated through a two-dimensional unsteady flow problem governed by the Navier-Stokes equations, highlighting its potential to expedite high-fidelity simulations in various scientific and engineering applications.

3Machine Learning-Based Digital Twin

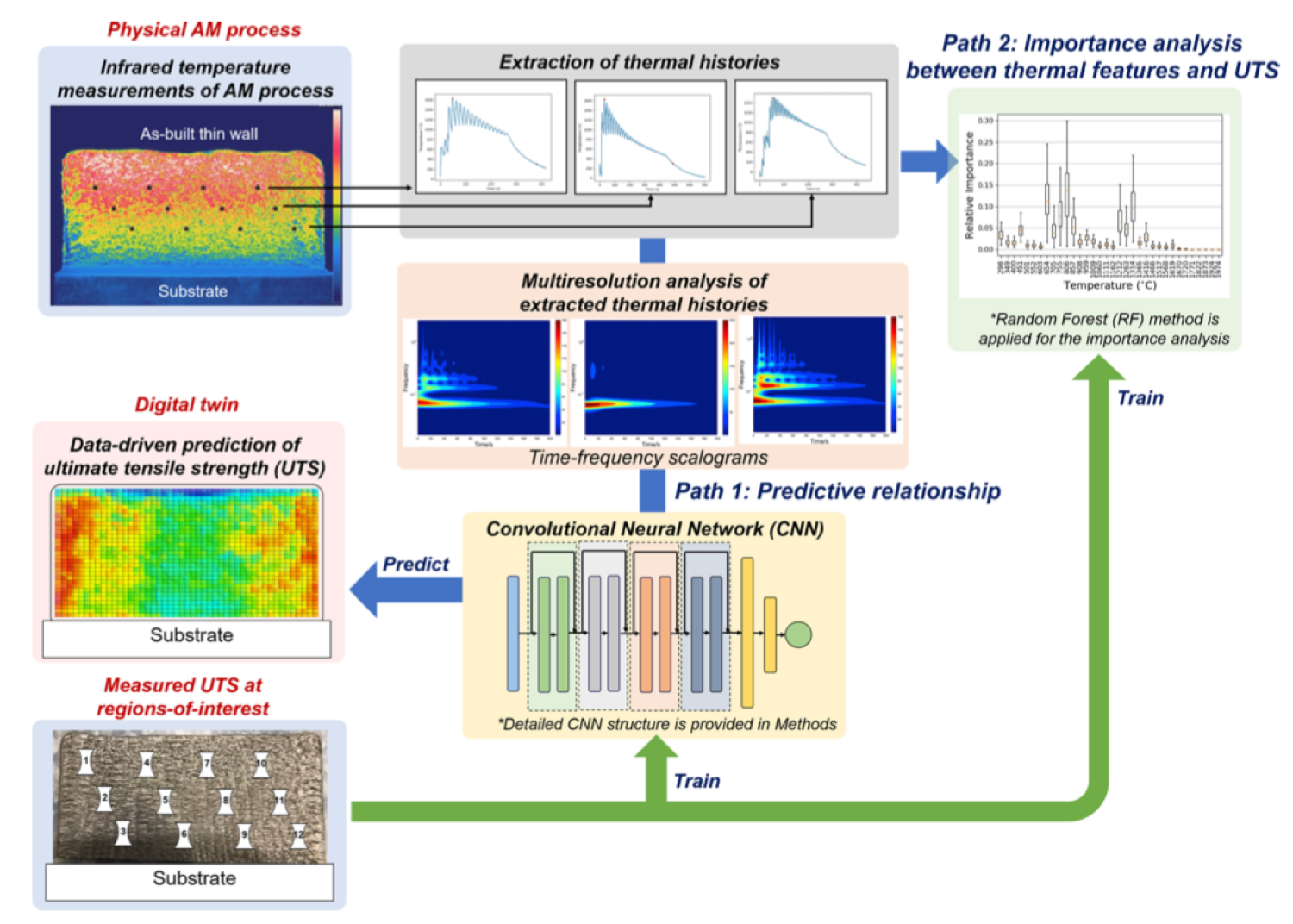
AI-Empowered Scientific Discovery and Digital Twin in Additive Manufacturing

Metal additive manufacturing provides remarkable flexibility in geometry and component design, but localized heating/cooling heterogeneity leads to spatial variations of as-built mechanical properties, significantly complicating the materials design process.

To address this challenge, we develop a mechanistic data-driven framework integrating wavelet transforms and convolutional neural networks to predict location-dependent mechanical properties over fabricated parts based on process-induced temperature sequences (thermal histories). The framework enables multiresolution analysis and importance analysis to reveal dominant mechanistic features underlying the additive manufacturing process, such as critical temperature ranges and fundamental thermal frequencies.

We systematically compare the developed approach with other machine learning methods. The results demonstrate that the developed approach achieves reasonably good predictive capability using a small amount of noisy experimental data. It provides a concrete foundation for a revolutionary methodology that predicts spatial and temporal evolution of mechanical properties leveraging domain-specific knowledge and cutting-edge machine and deep learning technologies.